树状数组

为了完成 计算右侧小于当前元素的个数，我们需要先了解一个全新的数据结构——树状数组。

考虑以下需求，对于一个数组，我们需要两个方法：

• add(idx, delta)

  我们需要对 arr[idx]，加上一个 delta 值。

• ask(idx)

  返回 arr[0:idx+1] 的总和。

我们容易想到下列两种解决方案

• 解决方案1——直接使用传统数组：

  这种方案下，add() 方法的时间复杂度是 $O(1)$$O(1)$，ask() 方法的时间复杂度是 $O(n)$$O(n)$

• 解决方案2——使用前缀和数组：

  前缀和数组是指，有这样一个数组 pre，其长度和传统数组 arr 一致。pre[i] 储存的是 sum(arr[0:i+1])。

  这种方案下，add() 方法的时间复杂度是 $O(n)$$O(n)$，因为我们需要更新每个受影响的前缀和的值，但是 ask() 方法的时间复杂度降低到了 $O(1)$$O(1)$

不管是上述解决方案中的哪种，在面对 n 次随机操作时，其期望的时间复杂度都是 $O(n^2)$$O(n^2)$，可以说是无法适应大数据量的。

那有没有什么办法可以将这两种操作的时间复杂度都变得很低呢？这就要使用树状数组了。

我们先来了解一个前置知识，什么是 lowbit。

lowbit 定义为非负整数 n 在二进制表示下最低位的 1 及其后面的所有的 0 的二进制构成的数值。

例如：

为了快速求得数字 n 的 lowbit 值，我们可以使用 n ^ ~n + 1。也即 n 取反加一，再和原 n 的值按位与。由于计算机里负数用的是补码表示负数，那么我们直接用 n ^ -n 即可求出 lowbit(n)

下面来正式介绍树状数组（图片来自视频）

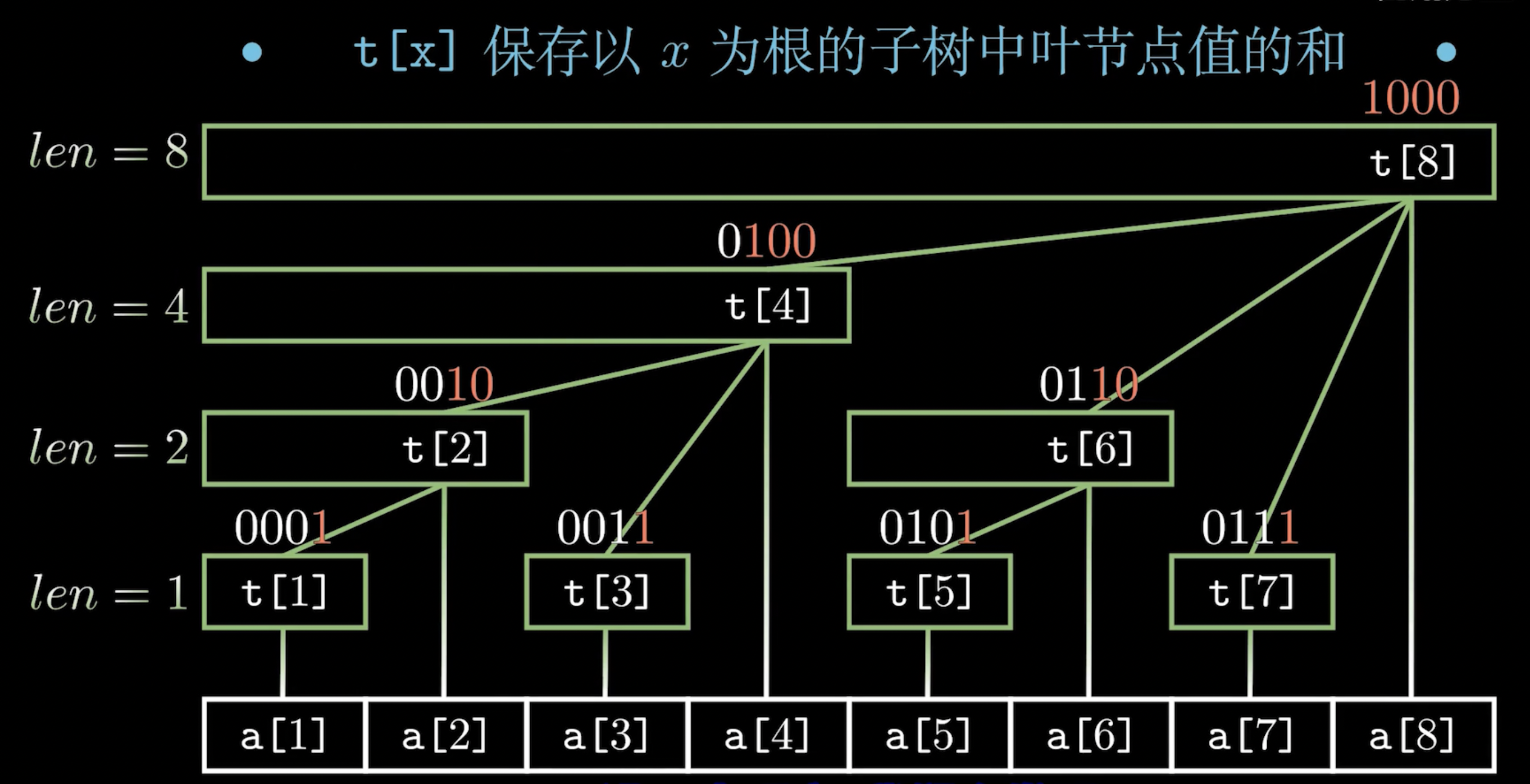
如图所示，这就是一个树状数组结构。

• t[x] 保存的是以 x 为根的子树中所有叶节点的和。这一点和 pre[x] 不同，t[x] 并没有直接保存前缀和。例如 t[3] 就只保存了 arr[3]。
• t[x] 保存了包括 arr[x] 在内的，往左一共 lowbit(x) 个数字的和。也就是说，t[x] 只管得到 lowbit(x) 个数字。
• 树状数组的高度为 ${\log }_2(n)+1$$\log_2(n) + 1$
• 注意：树状数组中，我们必须考虑将 1 作为起始位置，否则 lowbit 将不起作用！

在这种情况下，add() 和 ask() 方法都惊人地达到了 $O(\log n)$$O(\log n)$ 的时间复杂度，非常高效，这表明树状数组非常时候需要动态改变前缀和的情况。

下面给出代码：

'''
假设有树状数组 bitArr，其长度为 n
bitArr for Binary Indexed Tree Array
'''

def add(idx, delta):
    while idx < n:
        bitArr[idx] += delta
        idx += lowbit(idx)
           
def ask(idx):
    v = 0
    while idx >= 1:
        v += bitArr[idx]
        idx -= lowbit(idx)
    return v

结合上面的图片，我们来理解一下为什么代码是这样的

• 例如我们要运行 add(2, 1)

  那首先我们要另 t[2] += 1，然后，我们需要让受到影响的父节点 t[4] += 1，然后再另父节点的父节点 t[8] += 1

  可以发现，前缀和数组 pre 中，add(idx, delta)，会影响到 idx 之后的所有节点，所以是 $O(n)$$O(n)$ 复杂度，而树状数组中，则只会影响到二叉树的一支，所以复杂度是 $O(\log n)$$O(\log n)$

  另外，我们也知道了为什么要更新 idx += lowbit(idx)，因为这是在找它的父节点。

• 例如我们要运行 ask(7)

  根据图片，我们要凑齐 t[7] + t[6] + t[4] 才能凑出 pre[7]。那我们是怎么知道应该这么凑的呢？前文提到，t[x] 只能管得到包括 x 的往左一共 lowbit(x) 个数字的和，所以每次循环我们都更新 idx -= lowbit(idx)，因为减去 lowbit(idx)，正好就到了 idx 管不到的地方，这样一直加下去就能凑齐了。

树状数组的应用：

• 单点更新

  直接 add(idx, delta)

• 区间更新

  假设有这么一种情况，要求将 arr[i:j+1] 范围内的数字都加上 delta，应该怎么办？

  我们引入一个增量数组 b，初始情况下 b 为一个全零的数组。我们对 b 构造树状数组 bitArr，其初始情况是全零数组。

  此时，要求将 arr[i:j+1] 的范围内数字都加上 delta，则 add(i, delta) add(j+1, -delta)，则 ask(idx) 就是 arr[idx] 的增量。这是因为，要对 [i, j] 都加上 delta，那么就使得从 i 开始的前缀和加上 delta 即可，并且在 j + 1 开始，这个增量 delta 失效。

赣ICP备20003470号-4